بِسْــــــــــــــــــمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
1. PENGERTIAN RELASI • Diagram Panah • Himpunan Pasangan Berurutan • Diagram Cartesius2. PENGERTIAN FUNGSI3. MACAM FUNGSI
• Fungsi Konstan (tetap) • Fungsi Linier4. MENGHITUNG NILAI FUNGSI • Notasi Fungsi • Menghitung Nilai Fungsi • Menentukan Rumus Fungsi
MATEMATIKA KELAS VIII SEMESTER 1 : BAB 3 RELASI & FUNGSI
Relasi
Menyatakan hubungan antara suatu anggota himpunan dengan anggota himpunan lainnya. Himpunan A dan himpunan B dikatakan memiliki relasi jika ada anggota himpunan yang saling berpasangan. Relasi antara dua himpunan dapat dinyatakan dengan tiga cara yaitu dengan diagram panah, himpunan pasangan berurutan, dan diagram Cartesius.
1. Diagram Panah
Diagram panah merupakan cara yang paling mudah untuk menyatakan suatu relasi. Diagram ini membentuk pola dari suatu relasi ke dalam bentuk gambar arah panah yang menyatakan hubungan antara anggota himpunan A dengan anggota himpunan B.
Misalnya, ada 4 orang anak yaitu Ali, Siti, Amir dan Rizki. Mereka diminta untuk menyebutkan warna favorit mereka. Ali menyukai warna merah, Siti menyukai warna ungu, Amir menyukai warna hitam, dan Rizki menyukai warna merah. Dari hasil uraian tersebut, terdapat dua buah himpunan. Himpunan pertama adalah himpunan anak, kita sebut himpunan A dan himpunan yang kedua adalah himpunan warna, kita sebut himpunan B. Hubungan antara himpunan A dan himpunan B dapat di ilustrasikan dengan diagram panah seperti berikut:

Jadi, dapat disimpulkan bahwa diagram panah di atas merupakan relasi antara anak dengan warna yang mereka sukai. Relasi antara kedua himpunan tersebut dapat dinyatakan dengan panah-panah yang memasangkan anggota himpunan A dengan anggota himpunan B.
2. Himpunan Pasangan Berurutan
Selain dengan diagram panah, suatu relasi juga dapat dinyatakan dengan menggunakan himpunan pasangan berurutan. Caranya dengan memasangkan himpunan A dengan himpunan B secara berurutan. Kita dapat mengambil contoh dari contoh diagram panah tadi.
Ali menyukai warna merah
Siti menyukai warna ungu
Amir menyukai warna hitam
Rizki menyukai warna merah
Dari uraian di atas kita dapat menyatakan relasinya dengan himpunan pasangan berurutan seperti berikut:
(Ali, merah), (Siti, ungu), (Amir, hitam), (Rizki, merah).
Jadi, relasi antara himpunan A dengan himpunan B dinyatakan sebagai himpunan pasangan berurutan (x,y) dengan x ∈ A dan y ∈ B.
3. Diagram Cartesius
Menyatakan relasi antara dua himpunan dari pasangan berurutan yang kemudian dituliskan dalam bentuk dot (titik-titik). Contoh dari relasi antara anak dengan warna kesukaannya yaitu himpunan A = {Ali, Siti, Amir, Rizki} dan himpunan B = {merah, ungu, hitam}, dapat digambarkan dalam bentuk diagram Cartesius seperti di bawah ini:

Fungsi
Fungsi (pemetaan) merupakan relasi dari himpunan A ke himpunan B, jika setiap anggota himpunan A berpasangan tepat satu dengan anggota himpunan B. Semua anggota himpunan A atau daerah asal disebut domain, sedangkan semua anggota himpunan B atau daerah kawan disebut kodomain. Hasil dari pemetaan antara domain dan kodomain disebut range fungsi atau daerah hasil. Sama halnya dengan relasi, fungsi juga dapat dinyatakan dalam bentuk diagram panah, himpunan pasangan berurutan dan dengan diagram Cartesius.

Jadi, dari diagram panah di atas dapat disimpulkan:
Domain adalah A = {1,2,3}
Kodomain adalah B = {1,2,3,4}
Range fungsi = {2,3,4}
Sebuah fungsi dapat dinotasikan dengan huruf kecil sepeti f, g, h. Misal, fungsi f memetakan himpunan A ke himpunan B dinotasikan f(x) dengan aturan f : x → 3x+3. Artinya fungsi f memetakan x ke 3x+3. Jadi daerah bayangan x oleh fungsi f adalah 3x+3 sehingga dapat dinotasikan dengan f(x) = 3x+3. Dari uraian ini dapat dirumuskan:
Jika fungsi f : x → ax +b dengan x anggota domain f , maka rumus fungsif adalah f(x) = ax+b
Dengan menghitung nilai fungsi, kita dapat mengetahui nilai fungsi yang dapat menghasilkan himpunan kawan (kodomain) dari himpunan asal (domain). Supaya lebih jelas, coba kerjakan contoh soal di bawah ini.
Contoh Soal 1
Diketahui fungsi f : x → 3x + 3 pada himpunan bilangan bulat. Tentukan:
- f(3)
- bayangan (-2) oleh f
- nilai f untuk x = -4
- nilai x untuk f(x) = 6
- nilai a jika f(a) = 12
Pembahasan:
Fungsi f : x → 3x + 3
Rumus fungsi: f(x) = 3x+3
- f(3) = 3(3)+3 = 12
- bayangan (-2) oleh f sama dengan f (-2), jadi f(-2) = 3(-2)+3 = -3
- nilai f untuk x = -4 adalah f (-4) = 3(-4)+3 = -9
- nilai x untuk f(x) = 6 adalah
3x + 3 = 6
3x = 6-3
3x = 3
x = 1
5. nilai a jika f(a) = 12
3a + 3 = 12
3a = 12 – 3
3a = 9
a = 3
Contoh soal 2
Diketahui A = {1, 2, 3, 4} serta B = {1, 2, 3, 4, 5, 6, 7, 8}. Sebuah fungsi f: A → B ditentukan oleh f(x) = 2x – 1. Maka:
a. Gambarlah fungsi f dengan menggunakan diagram panah.
b. Tentukan range dari fungsi f.
c. Gambarlah grafik dari fungsi f
Pembahasan:
a. Diagram Panah
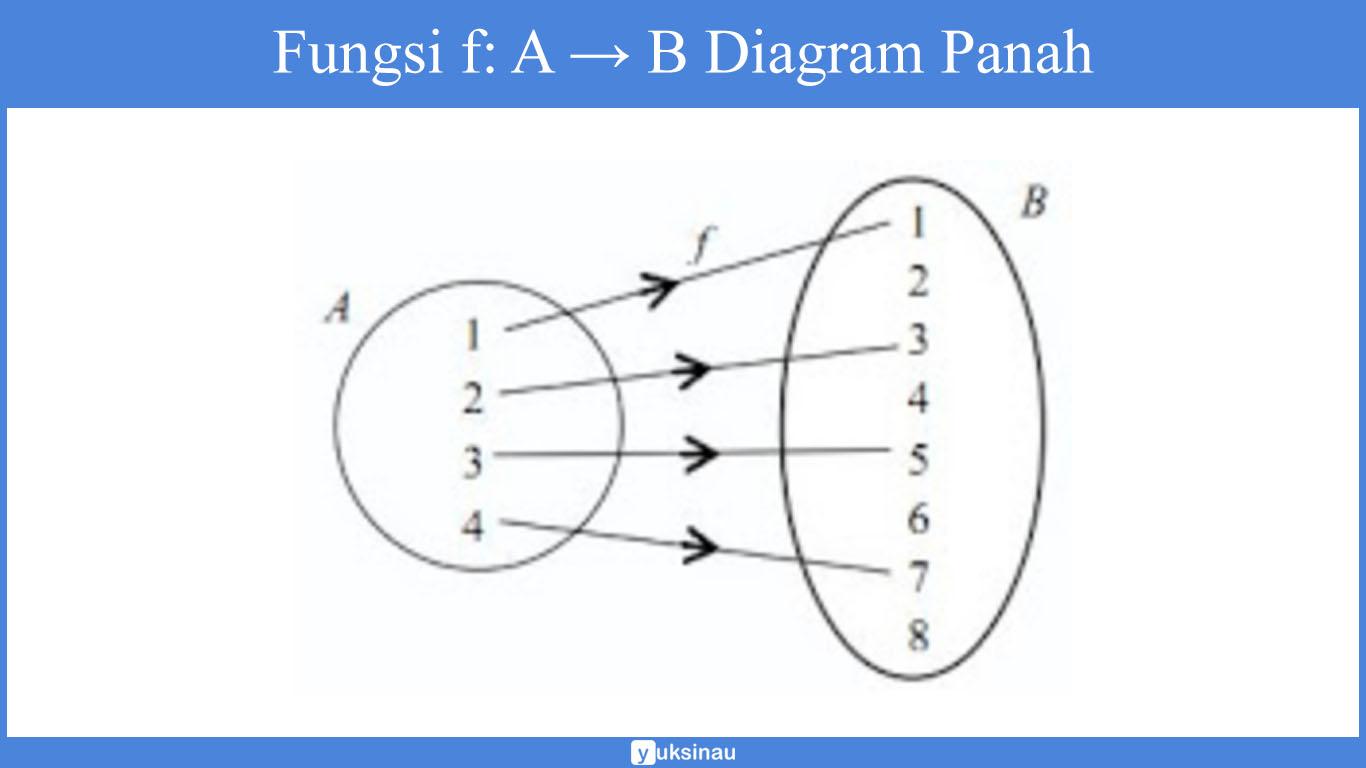
b. f(x) = 2x – 1
f(1) = 2.1 – 1 = 1
f(3) = 2.3 – 1 = 5
f(2) = 2.2 – 1 = 3
f(4) = 2.4 – 1 = 7
Sehingga, range dari fungsi f yaitu {1, 3, 5, 7}
c. Grafik fungsi

Macam-Macam Fungsi
1. Fungsi konstan (fungsi tetap)
Sebuah fungsi f: A → B ditentukan dengan rumus f(x) disebut sebagai fungsi konstan jika dalam setiap anggota domain fungsi selalu berlaku f(x) = C.
Yang mana C adalah bilangan yang konstan. Untuk lebih jelasnya dapat kalian lihat contoh di bawah ini.
Contoh soal 3
Diketahui f: R → R dengan rumus f(x) = 3 dengan daerah domain {x | -3 ≤ x < 2}. Maka tentukanlah gambar grafiknya dari fungsi di atas!
Pembahasan:

2. Fungsi linier
Fungsi linier adalah fungsi f(x) = ax + b, yang mana a ≠ 0, a dan b termasuk ke dalam bilangan konstan. Grafik linier berbentuk garis lurus. Untuk lebih jelasnya dapat kalian lihat contoh di bawah ini.
Contoh soal 4
Apabila diketahui f(x) = 2x + 3, maka tentukanlah gambar grafiknya.
Pembahasan:
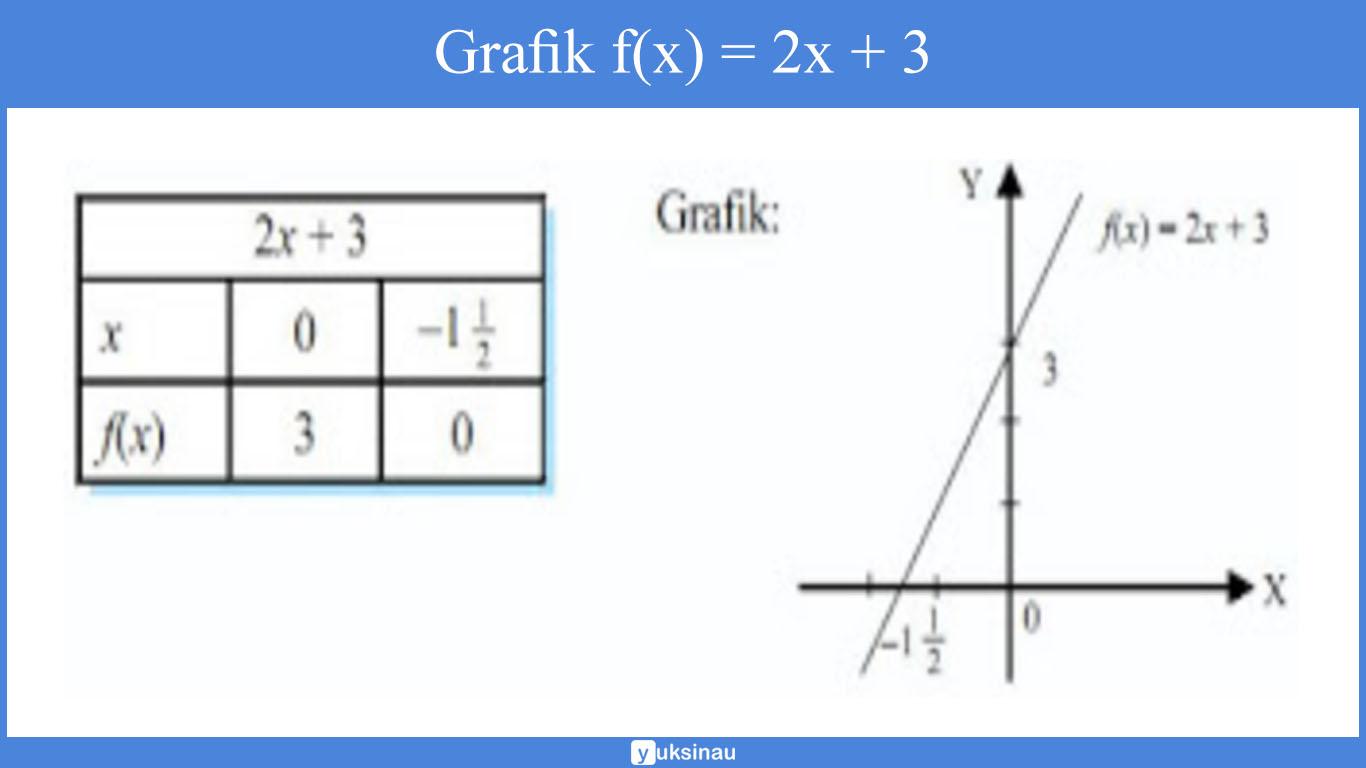
Menghitung Nilai dari Sebuah Fungsi
1. Notasi Fungsi
Sebuah fungsi dinotasikan dengan huruf kecil seperti f, g, h, i, dan sebagainya. Pada fungsi g yang memetakan himpunan A ke himpunan B dinotasikan dengan g(x). Misal ada fungsi f yang memetakan A ke B dengan aturan f : x → 2x + 2. Dari notasi fungsi tersebut, x merupakan anggota domain. fungsi x → 2x + 2 berarit fungsi f memetakan x ke 2x+2. Jadi daerah bayangan x oleh fungsi f adalah 2x + 2. Sobat dapat menotasikannya dengan f(x) = 2x +2. Kesimpulan
Jika fungsi f : x → ax + b dengan x anggota domain f maka rumus fungsi f adalah f(x) = ax +b
2. Menghitung nilai dari Sebuah Fungsi
Menghitung nilai dari sebuah fungsi cukup sederhana. Sobat hanya perlu mengikuti rules dari fungsi tersebut. Semakin susah fungsi yang memetakannya maka akan semakin susah menghitung nilai fungsinya. Terkadang soal-soal membalik fungsi tersebut, diketahui daerah hasil kemudian diminta mencari daerah asal. Yuk mari dismak contoh berikut:
Contoh Soal 5
Diketahui fungsi f : x → 2x – 2 dengan x anggota bilangan bulat. Coba sobat tentukan nilai dari
- f(3)
- f(4)
- bayangan (-3) oleh f
- nilai f untuk x = -10
- nilai a jika f(a) = 14
Pembahasan:
fungsi fungsi f : x → 2x – 2 dapat dinyatakan dengan f(x) = 2x – 2
- f(x) = 2x – 2
f(1) = 2(3) – 2 = 4 - f(x) = 2x – 2
f (4) = 2(4) – 2 = 6 - f(x) = 2x – 2
f(-3) = 2(-3) – 2 = -8 - f(x) = 2x – 2
f(10) = 2(10) -2 = 18 - f(a) = 2a – 2
14 = 2a -2
2a = 16
a = 8
3. Menentukan Rumus sebuah fungsi
Sebuah fungsi dapat sobat temukan rumusnya apabila ada nilai atau data yang diketehui. Kemudian dengan menggunakan aljabar sobat bisa dengan mudah menemukan rumus dari fungsi tersebut. Untuk lebih jelasnya bisa sobat simak contoh berikut:
Contoh Soal 6
Fungsi g yang berlaku pada himpunan bilangan riil ditentukan oleh rumus g(x) = ax + b dengan a dan b adalah bilangan bulat. Jika g(-2) = -4 dan g(1) = 5. Coba sobat tentukan nalai dari:
- nilai dari a dan b
- rumus fungsi
- g (-3)
Pembahasan
- Untuk mencari nilai a dan b kita buat persamaan dulu dari himpunan pasangan berurutan yang diketahui.
g(-2) = -4 → -4 = -2a + b → b = 2a – 4 …(1)
g(1) = 5 → 5 = a + b …(2)
kita substitusikan persamaan 1 ke persamaan 25
5
5
9
a= a + b
= a + 2a – 4
= 3a – 4
= 3a
= 3b = 2a – 4
b = 2(3) -4
b = 2
jadi nilai a = 3 dan b = 4 - rumus fungsinya g(x) = 3a + 2
- g(x) = 3a + 2
g(-3) = 3 (-3) + 2
g (-3) = -7
Contoh Soal & Pembahasan
Soal 1
Rumus suatu fungsi dinyatakan dengan f(x) = 2x + 5. Jika f(a) = 7, nilai a adalah ….
a. -1 c. 2
b. 1 d. 3
Pembahasan :
Rumus sebuah fungsi dinyatakan dengan f(x) = 2x + 5
f(a) = 7
maka
2a + 5 = 7
⇔ 2a = 7 – 5
⇔ 2a = 2
⇔ a = 1
Sehingga nilai a yaitu 1.
(jawaban b)
Soal 2
Diketahui rumus fungsi f(x) = -1-x. Nilai f(-2) adalah …
a. 3 c. -1
b. 1 d. -3
Pembahasan :
f(x) = -1-x
f(-2) = -1-(-2)
f(-2) = -1+2
f(-2) = 1
(jawaban b)
Soal 3.
Diketahui fungsi f(x) = 4x²+2x+5. Nilai f(½) = …
a. 6 c. 8
b. 7 d. 10
Pembahasan :
f(x) = 4x²+2x+5
f(½) = 4(½)²+2(½)+5
f(½) = 4(1/4) + 1 + 5
f(½) = 1 + 6
f(½) = 7
(jawaban b)
Soal 4
Suatu fungsi ditentukan dengan rumus f(x) = px + q. Jika f(-2) = 17 dan f(5) = -32, maka f(12) = …
a. -81 c. 29
b. -43 d. 87
Pembahasan :
f(x) = px + q
f(-2) = 17 → -2p + q = 17
f(5) = -32 → 5p + q = -32
__________________-
-7p = 49
p = 49/-7
p = -7
Substitusikan p = -7 ke salah satu persamaan, kita daoat memilih persamaan mana saja. Disini akan kita ambil -2p + q = 17, sehingga akan diperoleh:
-2p + q = 17
⇔ -2(-7) + q = 17
⇔ 14 + q = 17
⇔ q = 17 – 14
⇔ q = 3
Maka,
f(x) = px + q
f(x) = -7x + 3
f(12) = -7(12) + 3
f(12) = -84 + 3
f(12) = -81
(jawaban a)






Tidak ada komentar:
Posting Komentar