بِسْــــــــــــــــــمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
1. POLA BILANGAN • Pola bilangan ganjil • Pola bilangan genap • Pola bilangan persegi panjang • Pola bilangan persegi
• Pola bilangan segitiga
• Pola bilangan segitiga pascal
• Pola bilangan fibonacci
2. BARIS DAN DERET ARITMETIKA • Baris aritmetika
• Deret aritmetika
3. BARIS DAN DERET GEOMETRI
• Baris geometri • Deret geometri4. RANGKUMAN RUMUS
MATEMATIKA KELAS VIII SEMESTER 1 : BAB 1 POLA BILANGAN
Pengertian Pola Bilangan
Pola bilangan adalah susunan angka-angka yang membentuk pola tertentu, misalnya segitiga, garis lurus, persegi, dan masih banyak lainnya.
Macam-Macam Pola Bilangan
Adapun macam-macam pola bilangan adalah sebagai berikut.
1. Pola Bilangan Ganjil
Pola bilangan ganjil yaitu pola bilangan yang tersusun atas bilangan-bilangan ganjil. Ciri khas bilangan ganjil yaitu bilangan ini tidak habis dibagi dengan dua ataupun kelipatannya.
Barisan bilangan yang menunjukan pola bilangan ganjil ialah 1, 3, 5, 7, 9, 11 dan seterusnya.
Bentuk pola bilangan ganjil seperti gambar berikut.

Secara matematis untuk mencari rumus Un Pola bilangan ganjil suku ke-n.
1, 3, 5, 7, 9, 11, ….., n,
Rumus Un pola bilangan ganjil :
Un = 2n -1
2. Pola Bilangan Genap
Pola bilangan genap adalah pola bilangan yang tersusun dari kumpulan bilangan genap.
Contoh pola bilangan genap 2, 4, 6, 8, dan seterusnya.
Bentuk pola bilangan ganjil seperti gambar berikut.

Rumus pola bilangan genap ke-n
2, 4, 6, 8, 10,…,n
Un = 2n
3. Pola bilangan persegi panjang
Pola bilangan jenis ini akan menghasilkan bentuk menyerupai persegi panjang. Contohnya susunan angka 2, 6, 12, 20, 30, dan seterusnya. Untuk menentukan pola ke-n, kamu bisa menggunakan persamaan Un = n (n + 1) di mana n merupakan bilangan bulat positif. Jika digambarkan, pola bilangannya berbentuk seperti berikut.
Gambar di atas menunjukkan bahwa, susunan bilangan yang sedemikian sehingga memenuhi persamaan Un = n (n + 1) bisa membentuk suatu pola persegi panjang.
4. Pola bilangan persegi
Pola persegi adalah susunan bilangan yang dibentuk oleh bilangan kuadrat. Secara matematis, pola bilangan ini mengikuti bentuk Un = n2. Contoh susunan bilangan yang menghasilkan pola persegi adalah 1, 4, 9, 16, 25, 36, dan seterusnya. Jika dijabarkan dalam bentuk gambar, akan menjadi seperti berikut.
5. Pola bilangan segitiga
Dari namanya saja sudah bisa ditebak, kira-kira pola bilangannya akan membentuk bangun apa? Ya benar, segitiga. Segitiga yang dibentuk adalah segitiga sama sisi. Ada dua cara yang bisa Quipperian gunakan untuk membentuk pola ini, yaitu sebagai berikut.
a. Cara penjumlahan bilangan di mana selisih bilangan setelahnya +1 dari bilangan sebelumnya. Perhatikan contoh berikut.

Bilangan pada baris kedua (di dalam kotak berbingkai merah) merupakan selisih dari pola bilangan sebelum dan setelahnya. Kamu bisa melihat bahwa selisihnya selalu + 1 dari selisih sebelumnya. Kira-kira, bilangan setelah 15 berapa ya? Untuk memudahkan kamu menjawab, tentukan dulu selisih antara bilangan 15 dan setelahnya, yaitu +6. Jadi, bilangan setelah 15 adalah 15 + 6 = 21.
b. Cara kedua menggunakan rumus Un di mana Un = n⁄2 (n + 1).
Dengan cara ini, kamu bisa menentukan suku ke-n dengan lebih mudah.
Secara umum, pola segitiga ditunjukkan oleh gambar berikut.
6. Pola bilangan Pascal
Pola bilangan Pascal ini ditemukan oleh ilmuwan asal Prancis, yaitu Blaise Pascal. Jika dituliskan, pola bilangan Pascal akan membentuk suatu segitiga. Segitiga tersebut dinamakan segitiga Pascal. Ada beberapa ketentuan yang harus kamu tahu terkait pola bilangan Pascal, yaitu sebagai berikut.
- Baris paling atas (baris ke-1) diisi oleh angka 1.
- Setiap baris diawali dan diakhiri dengan angka 1.
- Setiap bilangan yang ditulis di baris ke-2 sampai ke-n merupakan hasil penjumlahan dari dua bilangan diagonal di atasnya (kecuali angka 1 pada baris ke-1).
- Setiap baris berbentuk simetris.
- Banyaknya bilangan di setiap barisnya merupakan kelipatan dua dari jumlah angka pada baris sebelumnya. Misalnya, baris ke-1 banyaknya bilangan = 1 maka baris ke-2 banyaknya bilangan = 2.
Adapun bentuk pola bilangan Pascal adalah sebagai berikut.
Gambar di atas menunjukkan bahwa pola bilangan Pascal itu sangat unik dan mudah sekali untuk dipahami. Untuk menentukan bilangan ke-n kamu bisa menggunakan persamaan 2n-1.
7. Pola Bilangan Fibonacci
Pola bilangan ini diperoleh dari menjumlahkan dua bilangan sebelumnnya. Rumus Un pola bilangan Fibonacci dinyatakan melalui rumus Un = Un-1 + Un-2.

Contoh pola bilangan Fibonacci : 1, 1, 2, 3, 5, 8, 13 dan seterusnya.
8. Pola Bilangan Aritmatika
Pola bilangan aritmatika yaitu bentuk dari barisan aritmatika yang memiliki selisih dua suku berdekatan selalu sama.
Bentuk umum barisan aritmatika.
U1, U2, U3, U4,….
a, a+b, a+2b, a+3b,….
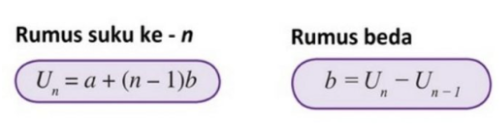
Dengan b= U2-U1=U4-U3 =Un – Un-1

Rumus suku ke-n adalah
Un = a+ (n-1)b
Rumus Baris Aritmatika
Keterangan :
Un = suku ke - n
a = suku pertama
b = beda/selisih
Rumus Deret Aritmatika
Keterangan :
Un = suku ke - n
Sn = jumlah n suku
a = suku pertama
b = beda/selisih
Rumus Baris Geometri
Keterangan :Un = suku ke - n
a = suku pertama
r = rasio
Rumus Deret Aritmatika
Keterangan :
Un = suku ke - n
Sn = jumlah n suku
a = suku pertama
r = rasio
RANGKUMAN MATERI BARISAN DAN DERET
A. Barisan dan Deret
Format Barisan 
Format Deret 
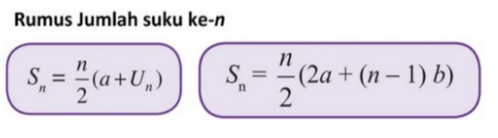
B. Rumus Deret Aritmetika
Suku ke-n 
Beda 
atau 
Jumlah n suku pertama
Jumlah n suku pertama 
Suku Tengah 
C. Rumus Deret Geometri
Rasio 
Suku ke-n 
Jumlah n suku pertama 
atau 
Suku Tengah (untuk banyak suku ganjil) 















Tidak ada komentar:
Posting Komentar