Oleh : Risa Gestiana
بِسْــــــــــــــــــمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
1. Pengertian PLSV
2. Bentuk PLSV
3. Cara Penyelesaian SPLSV
4. Contoh Soal & Pembahasan
MATEMATIKA KELAS VII SEMESTER 1 : BAB IV PLSV
Persamaan Linear Satu Variabel
Dari kata-kata "Persamaan Linear Satu Variabel", kita melihat adanya kata "Persamaan". Seperti yang kita ketahui bahwa :Persamaan merupakan suatu kalimat terbuka yang dihubungkan dengan simbol sama dengan (=) pada kedua ruasnya.
Sedangkan Pertidaksamaan merupakan kalimat terbuka yang dinyatakan dengan simbol -simbol yang menunjukkan pertidaksamaan, simbol-simbol tersebut seperti :
> = Lebih dari
< = Kurang dari
> = Lebih dari atau sama dengan
< = Kurang dari atau sama dengan
≠ = Tidak sama dengan
Kalimat Terbuka
Kalimat terbuka merupakan sebuah kalimat yang di dalamnya terkandung satu atau lebih variabel yang nilai kebenarannya belum diketahui. Contoh kalimat terbuka adalah :1. x + 2 = 15
2. x + 2y = 7
Persamaan No.1 memiliki satu variabel yaitu : x.
Persamaan No.2 memiliki dua variabel yaitu : x dan y.
Kedua persamaan diatas sama-sama disebut kalimat terbuka, namun karena ada persamaan yang memiliki satu variabel dan dua variabel. Maka ada yang disebut persamaan linear satu variabel dan persamaan linear dua variabel.
Persamaan Linear Satu Variabel
Persamaan Linear Satu Variabel adalah persamaan yang terdiri dari satu variabel dan pangkat terbesar dari variabel tersebut adalah satu.Bentuk Umum Persamaan Linear Satu Variabel:
ax + by = c, dengan a≠ 0
Catatan:
- Persamaan diatas memiliki satu variabel yaitu :x
- Pangkat dari variabel tersebut harus 1, terkadang tidak ditulis. Jadi x1 sama maksudnya dengan x (tanpa ditulis pangkatnya).
- Angka di depan variabel disebut sebagai koefisien
- Angka yang tidak memiliki variabel disebut konstanta. Misalkan 2x+5=0, memiliki konstanta 5.
- Seberapun banyak variabel sejenis yang ditulis, tetap persamaan tersebut dianggap satu variabelnya. Contoh 4x+5 = 2x + 2. Persamaan tersebut dianggap memiliki satu variabel, yaitu :x
Contoh Bentuk Persamaan Linear Satu Variabel
Yang manakah persamaan dibawah ini yang dianggap sebagai persamaan linear satu variabel?
a. 2x+ 5 = 10
b. x2+ 3x = 18
c. 2x + 2y = 8
d. x1/2+ 5 = 10
e. 2x +5 = 4x - 7
Penyelesaian:
a. Variabel pada persamaan 2x+ 5 = 10 adalah x dan berpangkat satu, maka persamaan linear satu variabel.
b. Variabel pada persamaan x2+ 3x = 18 adalah x yang memiliki pangkat satu dan dua, maka tidak termasuk persamaan linear satu variabel.
c. Variabel pada persamaan 2x + 2y = 8 adalah x dan y, karena terdapat dua variabel, maka tidak termasuk persamaan linear satu variabel.
d. Variabel pada persamaan x1/2+ 5 = 10 adalah x namun bukan berpangkat satu (berpangkat 1/2), maka tidak termasuk persamaan linear satu variabel.
e. Variabel pada persamaan 2x +5 = 4x - 7 adalah x. Walaupun terdapat variabel x pada ruas kiri dan ruas kanan, namun dianggap satu variabel yaitu :x. Oleh karena itu dianggap sebagai persamaan satu variabel juga.
Cara Penyelesaian SPLSV
Cara penyelesaian bentuk SPLSV adalah menghitung nilai numerik dari variabel-nya dengan memisahkan variabel dan konstanta sehingga masing-masing ruas hanya memuat variabel dan konstanta (tidak keduanya). Berikut cara penyelesaian persamaan linear satu variabel.
Memindahkan suatu elemen ke ruas lainnya artinya memberikan nilai lawan dari elemen tersebut ke ruas lainnya
Misalnya suatu persamaan 2x + 1 = 2, akan dipindahkan konstanta 1 di ruas kiri ke kanan.
2x + 1 = 5 (i) ⇔ 2x = 5 + (-1) (ii) ⇔ 2x = 5 - 1 (iii) ⇔ 2x = 4 (iv) terlihat pada langkah (ii) di ruas kanan ditambahkan dengan nilai -1 yang merupakan lawan dari konstanta 1 di ruas kiri.
Catatan: Tanda ⇔ merupakan operator logika ekuivalen, menyatakan bentuk semua persamaan di atas mempunyai solusi penyelesaian yang sama. # Mengapa hal ini terjadi? Sebenarnya untuk memindahkan suatu elemen dilakukan penghapusan nilai di ruas persamaan yang memuat elemen tersebut. Karena merupakan bentuk persamaan, jika terjadi penghapusan maka kedua ruas harus dilakukan penghapusan. Berikut dasar logikanya. 2x + 1 = 5 ⇔ 2x + 1 - 1 = 5 - 1 ⇔ 2x + 0 = 5 - 1 ⇔ 2x = 5 - 1 # Ingat mengurangkan sama artinya dengan menjumlahkan dengan angka negatif. 2x = 5 - 1 ⇔ 2x = 5 + (-1) Sehingga untuk mempercepat perhitungan, dapat langsung memberikan nilai lawannya. 2x + 1 = 5 ⇔ 2x = 5 - 1 ⇔ 2x = 4Perhitungan nilai variabel dilakukan dengan membagi setiap ruas dengan koefisien variabel-nya
Setelah masing-masing ruas disesuaikan sehingga masing-masing ruas hanya memuat variabel dan konstanta (tidak keduanya), baru perhitungan nilai variabel dilakukan. Hal ini dilakukan dengan membagi masing-masing ruas dengan nilai koefisien variabel yang dihitung.
Misalnya kelanjutan dari langkah sebelumnya telah ditemukan 2x = 4
Dilanjutkan dengan menghitung nilai x
Karena koefisien x adalah 2, masing-masing ruas dibagi dengan 2
2x = 4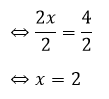
Sehingga solusi persamaan adalah nilai x = 2Memindahkan elemen variabel dilakukan secara menyeluruh termasuk koefisien-nya
Untuk memindahkan suatu variabel ke ruas lainnya, nilai koefisien variabel juga ikut dipindahkan.
Misalnya akan dipindahkan variabel x ke ruas lainnya dari persamaan
3x = 2x + 1
⇔ 3x - 2x = 1
⇔ x = 1
Jadi, solusi persamaan di atas adalah x = 1
Contoh Soal SPLSV
Berikut contoh soal SPLSV dan penyelesaiannya. Untuk memastikan solusi yang ditemukan benar, dapat dilakukan pengujian dengan substitusi (memasukkan) nilai x ke persamaan.
Tentukan solusi dari sistem persamaan linear 3x - 4 = 2
Jawaban: Solusi persamaan tersebut adalah x = 2
Untuk memastikan solusi yang diperoleh benar,
jika x = 2, maka substitusi 3x - 4 = 2 sebagai berikut
3x - 4 = 2
3.(2) - 4 = 2
6 - 4 = 2
2 = 2 (Benar)Tentukan solusi dari sistem persamaan linear x + 3 = 2x + 6
Jawaban: Solusi persamaan tersebut adalah x = -3
Untuk memastikan solusi yang diperoleh benar,
jika x = -3, maka substitusi x + 3 = 2x + 6 sebagai berikut
x + 3 = 2x + 6
(-3) + 3 = 2.(-3) + 6
0 = -6 + 6
0 = 0 (Benar)
Contoh Soal Cerita SPLSV
Eddy membeli 3 buku tulis dan sebuah pensil. Diketahui harga pensil adalah Rp 2.000 dan total belanja Rp 11.000. Hitunglah harga sebuah buku yang dibeli Eddy?
Diketahui:
3 Buku = 3x
Pensil = Rp 2.000
Total = Rp 11.000
Penyelesaian:
Dari informasi yang ada ditemukan satu variabel buku yaitu x yang akan dicari. Sehingga dapat digunakan sistem persamaan linear satu variabel pada permasalahan di atas.
3 Buku + Pensil = Total
3x + Rp 2.000 = Rp 11.000
3x = Rp 11.000 - Rp 2.000
3x = Rp 9.000
(3x)/3 = Rp 9.000/3
x = Rp 3.000
Buku = Rp 3.000
Jawaban: Harga buku yang dibeli Eddy adalah Rp 3.000 per buah
Untuk memastikan harga buku, dapat dilakukan substitusi harga buku
3 Buku + Pensil = Total
(3 × Rp 3.000) + Rp 2.000 = Rp 11.000
Rp 9.000 + Rp 2.000 = Rp 11.000
Rp 11.000 = Rp 11.000 (Benar)
Contoh Soal & Pembahasan
1. Tentukan persamaan dari 2x - 1 = 5 ?Penyelesaian :
2x - 1 = 5
2x = 5 + 1
2x = 6
x = 32. Berapakah nilai x dari persamaan : 3(x – 1) + x = –x + 7.
Penyelesaian :
3(x – 1) + x = –x + 7
3x - 3 + x = -x + 7
4x - 3 = -x + 7
4x + x = 7 + 3
5x = 10
x = 10/5
x = 23. Berapa nilai y dari persamaan : 28 y = 18
Penyelesaian :
28 y = 18
2y = 18 . 8
y = 9 . 8
y = 72
4. Tentukan nilai n dari persamaan : 2n + 2 = 12
Penyelesaian:
2n + 2 = 12
2n = 12 - 2
2n = 10
n = 55. Umur ibu 3 kali umur anaknya. Selisih umur mereka adalah 30 tahun. Berapakah umur anak dan ibunya ?
Penyelesaian :
Diketahui :
Umur ibu tiga kali umur anakanya
Misal: umur anaknya x tahun,
Maka : umur ibunya = 3x tahun.
Selisih umur mereka 30 tahun, jadi persamaannya adalah
3x – x = 30
2x = 30
x = 15
Jadi, umur anaknya 15 tahun dan ibunya (3 x 15) tahun = 45 tahun.6. Bu tini menyuruh Budi membeli gula pasir sebanyak 3 kg. Sesampainya Budi di toko Pak Tono, Budi menyerahkan uang Rp 50.000,00 untuk 3 kg gula pasir dan menerima uang kembalian sebesar Rp 11.000,00. Berapakah harga gula pasir untuk per-kg nya ?
Pembahasan
Misalkan : x = harga gula pasir
Budi menyerahkan uang Rp 50.000,00 untuk 3 kg gula pasir
dan menerima uang kembalian sebesar Rp 11.000,00
dapat kita buat persamaannya menjadi :
3 kg × harga gula = 50.000 − 11.000
3x = 50.000 − 11.000
Sekarang tinggal kita cari nilai x-nya :
3x = 50.000 − 11.000
3x = 39.000
x = 11.000
Jadi harga gula pasir per-kg adalah Rp 11.0007. Amir memiliki kelereng sebanyak a. Budi memiliki kelereng 10 buah lebih sedikit dari kelereng Amir. Jika jumlah kelereng mereka adalah 30, pernyataan berikut yang benar adalah…
A. a + 10 = 30
B. a – 10 = 30
C. 2a + 10 = 30
D. 2a = 40
Pembahasan :
Kelereng Amir = a
Kelereng Budi = a – 10
Kelereng Amir + Kelereng Budi = 30
a + a – 10 = 30
2a – 10 = 30
2a = 30 + 10
2a = 40
Jawab: D. 2a = 40
8. Persegipanjang ABCD memiliki ukuran panjang 4 cm lebihnya dari lebar. Jika keliling persegi panjang ABCD adalah 48 cm, tentukan:
a) lebar persegipanjang
b) panjang persegipanjang
c) luas persegipanjang
Pembahasan :
lebar → l = l
panjang → p = l + 4
Keliling adalah 2 x jumlah panjang dan lebar.
2(p + l) = 48
p + l = 48/2
p + l = 24
Karena panjang p = l + 4 maka
a) lebar persegipanjang
p + l = 24
l + 4 + l = 24
2l = 24 – 4
2l = 20
l = 20/2 = 10 cm
b) panjang persegipanjang
panjang = l + 4
= 10 + 4 = 14 cm
c) luas persegipanjang
Luas = p x l
= 14 x 10
= 140 cm²
Tidak ada komentar:
Posting Komentar