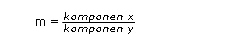MATRIKS ORDO 3X3

Oleh : Risa Gestiana

Riie.com

بِسْــــــــــــــــــمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ

Menentukan Invers Matriks Ordo 3x3

Menentukan matriks invers ordo 3x3 ada 2 cara, yaitu:

1. Metode mereduksi elemen baris
2. Metode minor-kofaktor

Berikut ini adalah 5 langkah menentukan invers matriks ordo 3x3 dengan menggunakan metode minor-kofaktor, diantaranya adalah :

1. Tentukan minor matriks
2. Tentukan kofaktor matriks 
3. Tentukan adjoin matriks
4. Tentukan determinan matriks
5. Operasikan rumus invers matriks

1. Minor

Gambar di atas memperlihatkan minor matriks 3×3, yaitu:

• Minor a =

• Minor e = 

• Minor h = 
• Dst.

2. Kofaktor

Kofaktor matriks 3×3 yaitu +a, -b, +c, -d, +e, -f, +g, -h, +i.

3. Adjoin

Adjoin diperoleh dari transpose suatu matriks.

Caranya mudah, yaitu… diagonal utama sebagai sumbu putar.

Putar berlawanan arah jarum jam dan… didapatlah Adjoin!

4. Determinan 

Jika determinan = 0, maka matriks tidak mempunyai invers.

5. Invers

Invers matriks memiliki rumus sebagai berikut :

Contoh Soal & Pembahasan :

Tentukan invers dari matriks dibawah ini !

Pembahasan :
Untuk menjawab soalnya maka kita praktikan langkah-langkah di atas :

1. Minor

Maka minor-minornya nya adalah :

a. Minor baris ke-1, kolom ke-1 :

b. Minor baris ke-1, kolom ke-2 :

c. Minor baris ke-1 kolom ke-3 :

d. Minor baris ke-2, kolom ke-1 :

e. Minor baris ke-2, kolom ke-2 :

f. Minor baris ke-2, kolom ke-3 :

g. Minor baris ke-3, kolom ke-1 :

h. Minor baris ke-3, kolom ke-2 :

i. Minor baris ke-3, kolom ke-3 :

Maka minor dari matriks A adalah :

2. Kofaktor

karena minornya sudah diketahui maka kita cari kofaktor matriks dari minor yang telah diketahui, maka :

Maka kofaktornya adalah :

3. Adjoin

Untuk menentukan adjoinnya kita trasnposekan kofaktor matriksnya.

maka adjoinnya adalah :

4. Determinan

maka determinannya adalah:

5. Invers

Pada langkah terakhir ini kita tinggal langsung mengoperasikan rumus invers :

maka :

PERSAMAAN GARIS LURUS

Oleh : Risa Gestiana

Riie.com

بِسْــــــــــــــــــمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ

Rangkuman materi belajar online Matematika VIII semester 1 Bab IV : Persamaan Garis Lurus

1. Pengertian & Bentuk Persamaan Garis Lurus

    • Pengertian persamaan garis lurus

    • Bentuk persamaan garis lurus

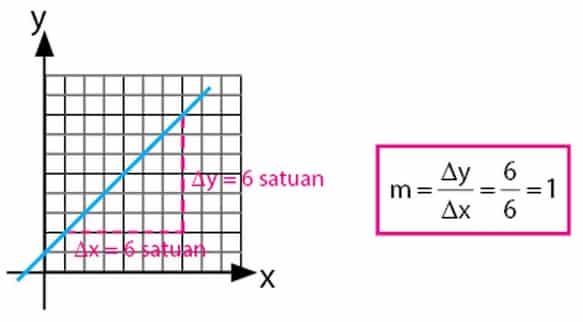
2. Gradien (m)

    • Sejajar

    • Tegak Lurus

3. Menentukan Persamaan Garis Lurus

    • Melalui satu titik

    • Melalui dua titik

Uji Kompetensi Bab 4 : Persamaan Garis Lurus

(Pilihan ganda halaman 42 nomor 1-15)

1.  Gradien garis lurus dengan persamaan 6x + 24y + 5 = 0 adalah ...

a. 1/4

b. - 1/4

c. 4

d. -4

2.  Persamaan garis lurus melalui titik (4, -3) dan (5, -6) adalah ...

a. 3x + y = -15

b. 3x + y = 9

c. 3x - y = 15

d. 3x - y = -9

3.  Persamaan garis lurus melalui titik (2, -5) sejajar dengan garis 4x + 2y - 15 = 0 adalah ...

a. 2x + y + 1 = 0

b. -2x - y + 1 = 0

c. 2x + 2y + 1 = 0

d. 2x + y - 1 = 0

4.  Persamaan garis melalui titik (3, -4) tegak lurus dengan garis 5x + 10y + 18 = 0 adalah ...

a. 2x - y = 10

b. -2x - y = -10

c. 2x + y = 10

d. 2x - y = -10

5. Gradien garis melalui titik O(0, 0) dan B(-7, 5) adalah ...

a. -5

b. -7

c. - 5/7

d. - 4/7

6.  Gradien garis m pada gambar berikut adalah ...

a. 1

b. - 1/4

c. -1

d. 4

7.  Gradien garis dari persamaan -5x + 2y + 6 = 0 adalah ...

a. 5

b. 5/2

c. 2

d. 2/5

8.  Persamaan garis melalui titik A(-2, 2) dan titik B(2, 7) adalah ...

a. 4y = 5x - 18

b. 4y = 5x + 18

c. 4y = 5x - 2

d. 4y = 5x + 2

9.  Besar gradien dari garis yang melalui titik (3, -4) dan (-7, 1) adalah ...

a. - 1/2

b. 1/2

c. 1

d. 2

10. Persamaan garis yang melalui titik (3, 1) dan sejajar dengab garis y = 2x + 3 adalah ...

a. y = -2x - 5

b. y = -2x + 5

c. y = 2x - 5

d. y = 2x + 5

11. Hubungan antara garis 4y = 6x - 8 dengan 2x + 3y = 6 adalah ...

a. sejajar

b. berimpitan

c. tegak lurus

d. berpotongan

12. Persamaan garis l yang melalui titik A(3, -2) dengan gradien garis m = -5 adalah ...

a. y = -5x + 13

b. y = 5x + 13

c. y = 5x - 13

d. y = -5x - 13

13. Persamaan garis yang melalui titik P(-1, 0) dan Q(3, -8) adalah ...

a. y = 2x + 2

b. y = 2x + 1

c. y = -2x - 2

d. y = 2x - 1

14. Persamaan garis yang melalui titik A (4, -1) dan sejajar dengan garis y = 3x + 2 adalah ...

a. y = 2x + 13

b. y = 1/3 x + 6

c. y = 3x - 13

d. y = 1/2 x + 4

15. Persamaan garis melalui titik (-2, 3) dan mempunyai gradien m = 1/2 adalah ...

a. y = 1/2 x - 2

b. y = 1/2 x + 2

c. y = 1/2 x - 4

d. y = 1/2 x + 4

Kunci Jawaban Uji Kompetensi Bab 4 : Persamaan Garis Lurus

Silahkan unduh kunci jawaban pada link berikut :

Kunci jawaban uji kompetensi Bab 4 : Persamaan Garis Lurus PG halaman 42 nomor 1-15

Latihan Soal Bab 4 : Persamaan Garis Lurus

(Esai halaman 43 nomor 1-10)

1.  Gradien garis yang melalui titik A(-3, 4p) dan B(9, p) adalah 2. Nilai 1/2 p = ...

2.  Persamaan garis yang melalui titik (-4, 7) dan titik (10, -1) adalah ...

3.  Persamaan garis yang melalui titik (4, 3) dan sejajar dengan garis 2x = y + 5 adalah ...

4.  Persamaan garis lurus yang sejajar dengan garis -3x + y - 2 = 0 dan melalui titik (3, -1) adalah ...

5.  Persamaan garis yang melalui titik (3, 4) dan (2, 5) adalah ...

6.  Kedudukan garis g1 : 2y = 3x + 8 dan garis g2 : 6y = 2x - 12 adalah ...

7.  Persamaan garis yang melalui titik (3, -2) dan bergradien - 1/3 adalah ...

8.  Persamaan garis g : 3x + 5 = 6y. Gradien garis yang tegak lurus dengan garis g adalah ...

9.  Persamaan garis yang melalui titik (-1, 2) dan tegak lurus dengan garis g adalah ...

10. Gradien garis 6y = 2x + 12 adalah ...

PERSAMAAN GARIS LURUS

Oleh : Risa Gestiana

Riie.com

بِسْــــــــــــــــــمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ

Materi belajar online Matematika VIII semester 1 :

1. Pengertian & Bentuk Persamaan Garis Lurus

    • Pengertian persamaan garis lurus

    • Bentuk persamaan garis lurus

2. Gradien (m)

    • Sejajar

    • Tegak Lurus

3. Menentukan Persamaan Garis Lurus

    • Melalui satu titik

    • Melalui dua titik

MATEMATIKA KELAS VIII SEMESTER 1 : BAB 4 PERSAMAAN GARIS LURUS

1. Persamaan Garis Lurus

Persamaan Garis lurus yaitu suatu perbandingan antara koordinat y dan koordinat x dari dua titik yang terletak pada sebuah garis.

Sedangkan garis lurus sendiri ialah kumpulan dari titik–titik yang sejajar. Dan garis lurus dapat dinyatakan dalam berbagai bentuk.

Dibawah ini beberapa contoh untuk menyatakan persamaan garis lurus, yaitu :

• y = mx + c
• y = -mx + c
• y = ax
• x = a
• ax + by = c
• ax – by = -c
• ax + by + c = 0
• dan lain-lain

2. Gradien (m)

Gradien yaitu Perbandingan komponen y dan komponen x , atau disebut juga dengan kecondongan sebuah garis. Lambang dari suatu gradien yaitu huruf “m”.

Gradien juga dapat dinyatakan sebagai nilai dari kemiringan suatu garis dan dapat dinyatakan dengan perbandingan Δy/Δx

Perhatikan gambar dibawah ini untuk menentukan gradien pada sebuah persamaan garis berikut :

Cara Menentukan Gradien

Berikut ini rumus mencari gradien garis dengan beberapa jenis persamaan :

• Gradien dari persamaan ax + by + c = 0

•  Gradien yang melalui titik pusat ( 0 , 0 ) dan titik ( a , b )m = b/a

• Gradien Yang melalui titik  ( x1 , y 1 ) dan ( x2 , y2 )

• Gradien garis yang saling sejajar  ( / / )

m = sama atau jika dilambangkan adalah m₁ = m₂

• Gradien garis yang saling tegak lurus ( lawan dan kebalikan )

m = -1 atau  m₁ x m₂ = -1

3. Menentukan Persamaan Garis Lurus

Ada dua hal yang perlu diperhatikan saat ingin membuat persamaan garis lurus. Pertama, kamu harus tahu nilai gradien m dari garis tersebut dan kedua, kamu harus tahu sedikitnya satu titik yang dilalui garis itu. Berikut ini merupakan dua kondisi yang dapat dicari tahu bentuk persamaan garis lurusnya.

1) Jika diketahui gradien dan satu titik yang dilalui garis

Misalnya, suatu garis melalui sebuah titik, yaitu (x₁,y₁). Kamu dapat menentukan persamaan garis lurusnya dengan rumus:

Contoh:

Tentukan persamaan garis yang bergradien 3 dan melalui titik (-2,-3)!

Penyelesaian:

Diketahui m = 3 dan (x₁,y₁) = (-2,-3). Sehingga,

Jadi, persamaan garis lurusnya adalah y = 3x + 3.

2) Jika diketahui dua titik yang dilalui garis

Misalnya, suatu garis melalui dua buah titik, yaitu (x₁,y₁) dan (x₂,y₂). Kamu bisa menggunakan rumus di bawah ini untuk mengetahui persamaan garisnya.

Contoh Soal & Pembahasan

Latihan Soal Matematika Kelas VIII

Kerjakan dibuku tulis seperti contoh diatas!

1. Tentukan gradien garis yang sejajar garis :

     x + 4y + 5 = 0

2. Tentukan gradien garis yang tegak lurus garis :

     y = -x - 5

3. Tentukan persamaan garis yang melalui titik B(-4, 0) dan sejajar garis 2x + 3y = 1

4. Tentukan persamaan garis yang melalui titik A(2, 5) dan tegak lurus garis y = -1/2 x + 6

5. Tentukan persamaan garis yang melalui titik A(3, -2) dan B(-1, 3)!