Oleh : Risa Gestiana
MATEMATIKA KELAS VIII SEMESTER 1 : BAB 4 PERSAMAAN GARIS LURUS
1. Persamaan Garis Lurus
Persamaan Garis lurus yaitu suatu perbandingan antara koordinat y dan koordinat x dari dua titik yang terletak pada sebuah garis.
Sedangkan garis lurus sendiri ialah kumpulan dari titik–titik yang sejajar. Dan garis lurus dapat dinyatakan dalam berbagai bentuk.
Dibawah ini beberapa contoh untuk menyatakan persamaan garis lurus, yaitu :
- y = mx + c
- y = -mx + c
- y = ax
- x = a
- ax + by = c
- ax – by = -c
- ax + by + c = 0
- dan lain-lain
2. Gradien (m)
Gradien yaitu Perbandingan komponen y dan komponen x , atau disebut juga dengan kecondongan sebuah garis. Lambang dari suatu gradien yaitu huruf “m”.
Gradien juga dapat dinyatakan sebagai nilai dari kemiringan suatu garis dan dapat dinyatakan dengan perbandingan Δy/Δx
Perhatikan gambar dibawah ini untuk menentukan gradien pada sebuah persamaan garis berikut :
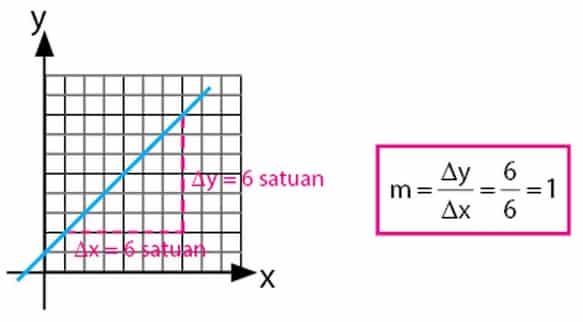
Berikut ini rumus mencari gradien garis dengan beberapa jenis persamaan :
- Gradien dari persamaan ax + by + c = 0
- Gradien yang melalui titik pusat ( 0 , 0 ) dan titik ( a , b )m = b/a
- Gradien Yang melalui titik ( x1 , y 1 ) dan ( x2 , y2 )
- Gradien garis yang saling sejajar ( / / )
m = sama atau jika dilambangkan adalah m1 = m2
- Gradien garis yang saling tegak lurus ( lawan dan kebalikan )
m = -1 atau m1 x m2 = -1
3. Menentukan Persamaan Garis Lurus
Ada dua hal yang perlu diperhatikan saat ingin membuat persamaan garis lurus. Pertama, kamu harus tahu nilai gradien m dari garis tersebut dan kedua, kamu harus tahu sedikitnya satu titik yang dilalui garis itu. Berikut ini merupakan dua kondisi yang dapat dicari tahu bentuk persamaan garis lurusnya.
1) Jika diketahui gradien dan satu titik yang dilalui garis
Misalnya, suatu garis melalui sebuah titik, yaitu (x1,y1). Kamu dapat menentukan persamaan garis lurusnya dengan rumus:

Contoh:
Tentukan persamaan garis yang bergradien 3 dan melalui titik (-2,-3)!
Penyelesaian:
Diketahui m = 3 dan (x1,y1) = (-2,-3). Sehingga,

Jadi, persamaan garis lurusnya adalah y = 3x + 3.
2) Jika diketahui dua titik yang dilalui garis
Misalnya, suatu garis melalui dua buah titik, yaitu (x1,y1) dan (x2,y2). Kamu bisa menggunakan rumus di bawah ini untuk mengetahui persamaan garisnya.



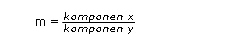










Tidak ada komentar:
Posting Komentar