Oleh : Risa Gestiana

Riie.com

بِسْــــــــــــــــــمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ

Materi belajar online Kimia XII semester 1 :

1. Pengertian Unsur Radioaktif

2. Sinar Radioaktif

    • Alfa

    • Beta

    • Gamma

3. Stabilitas Inti

4. Peluruhan

5. Kecepatan Peluruhan

UNSUR RADIOAKTIF

A. Pengertian Unsur Radioaktif

Unsur Radioaktif adalah unsur yang dapat memancarkan radiasi secara spontan.

Radiasi adalah sejenis sinar tetapi memiliki energi yang besar dan daya tembus yang tinggi.

Radiasi yang dipancarkan zat radioaktif terdiri dari 3 jenis partikel:

• Sinar alfa   ₂a⁴
• Sinar beta _-1b ⁰
• Sinar gama  ₀g ⁰

Pada tahun 1895, Roentgen menemukan sinar X, suatu radiasi elektromagnet berenergi tinggi yang dapat menghitamkan pelat potret meski masih terbungkus kertas hitam. Hingga kini sinar X digunakan untuk roentgen.

Pada tahun 1896, Herny Becquerel meneliti radiasi yang dipancarkan oleh batuan yang dapat berpendar. Secara kebetulan, Becquerel menemukan bahwa uranium senantiasa memancarkan radiasi secara spontan. Fenomena ini dinamakan radioaktivitas.

Pada tahun 1898, pasangan suami istri Pierre dan Marie Curie menemukan dua unsur radioaktif lainnya, yaitu radim dan polonium. Ternyata banyak unsur yang secara alami bersifat radioaktif. Semua isotop yang bernomor atom di atas 83 atau kurang mempunyai isotop yang stabil, kecuali teknesium dan promesium. Isotop yang bersifat radioaktif disebut isotop radioaktif atau radioisotop, sedangkan isotop yang tidak radio aktif disebut isotop stabil.

Persamaan inti

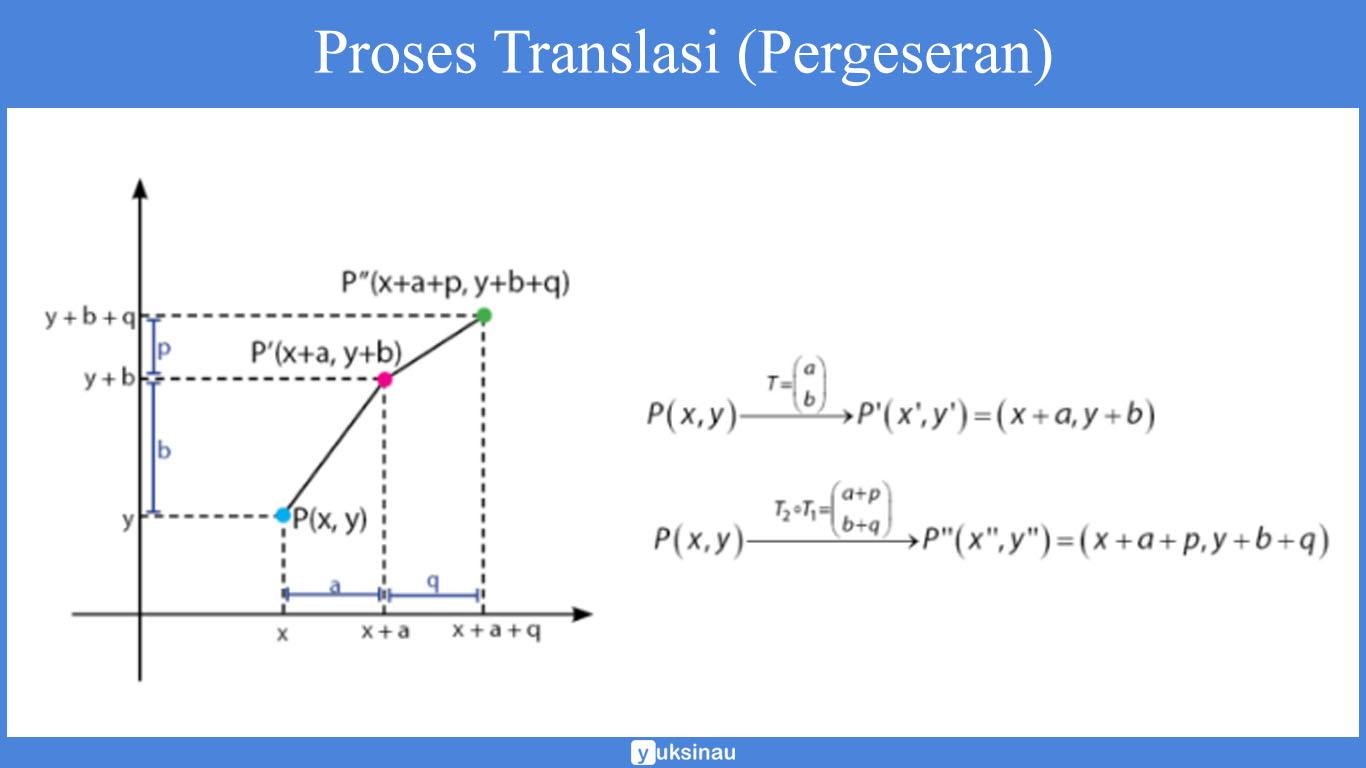
Pemancaran radiasi oleh unsur radioaktif disebut peluruhan (disintegrasi). Proses peluruhan dipaparkan dengan suatu persamaan yang disebut persamaan inti (nuclear equation).

Persamaan ini  juga mengikuti azas kesetaraan. Suatu persamaan ini dikatakan setara jika muata (nomor atom) dan massa di ruas kiri sama dengan di ruas kanan. Untuk contoh di atas:

Jumlah muatan di ruas kiri = 92 ; di ruas kanan = 90 + 2 = 92

Nomor massa di ruas kiri = 238 ; di ruas kanan = 234 + 4 = 238

Transmutasi buatan ( Artificial Transmutation )

Transmutasi atau perubahan suatu nuklida menjadi nuklida lain terjadi pada peluruhan radioaktif. Transmutasi dapat juga terjadi pada inti stabil, yaitu jika ditembaki dengan peluru atomer, seperti partikel alfa, neutron, atau suatu inti ringan. Transmutasi yang dilakunan dengan itu disebut Transmutasi buatan.

Transmutasi buatan pertama kali diamati oleh Ernest Rutherford pada tahun 1919 ketika ia mempelajari penembakan unsur ringan dengan partikel alfa.

Reaksi yang terjadi adalah sebagai berikut :

Reaksi transmutasi biasanya diringkaskan dengan notasi sebagai berikut.

T(x,y)P

Dengan, T= inti sasaran

x= partikel yang ditembakan

y= partikel hasil

p= inti baru

Laju peluruhan waktu paro

Peluruhan tergolong reaksi orde satu, kelajuannya hanya bergantung pada jumlah nuklida radioaktif. Secara matematis, laju peluruhan dinyatakan dengan persamaan sebagai berikut

Dengan  = laju peluruhan ( kereaktifan ), yaitu banyaknya peluruhan dalam satu satuan waktu

= tetapan peluruhan ( serupa dengan k dalam persamaan laju reaksi), nilainya bergantung pada jenis radioisotop.

N = jumlah nuklida radioaktif dalam contoh.

Waktu paro adalah waktu yang diperlukan sehingga separo zat radioaktif meluruh. Salah satu ciri reaksi berorde satu adalah bahwa waku paronya tidak bergantung pada jumlah zat mula-mula. Berapapun jumlah radio-isotop mula-mula, selalu diperlukan waktunyang sama sehingga separo daripadanya meluruh.

Dengan mengetahui waktu paro, kita dapat meramalkan sisa zar radioaktif setelah selang waktu tertentu. Hubungan antar fraksi zat yang tersisa dengan waktu paro dari rumus sebagai berikut.

Nt/No=(1/2)ⁿ

N_o = jumlah zat radioaktif mula-mula

N_t = jumlah zat radioaktif yang masih tersisa pada waktu t

n =t/t1/2= waktu/ waktu paro

oleh karena kereaktifan sebanding dengan jumlah atom radioaktif maka persamaan diatas dapat juga ditulis sebagai berikut 

At/Ao= (1/2)ⁿ

A_t = kereaktifan pada waktu t

A_o = kereaktifan awal

B. Sinar Radioaktif

Sinar yang dipancarkan oleh unsur radioaktif memiliki sifat-sifat:

1. dapat menembus lempeng logam tipis;

2. dapat menghitamkan pelat film;

3. dalam medan magnet terurai menjadi tiga berkas sinar.

Pada tahun 1898 Paul Ulrich Villard menemukan sinar radioaktif yang tidak dipengaruhi oleh medan magnet yaitu sinar gamma (γ ). Setahun kemudian Ernest Rutherford berhasil menemukan dua sinar radioaktif yang lain, yaitu sinar alfa (α ) dan sinar beta ( β ).

1. Sinar Alfa (α)

Sinar alfa merupakan inti helium (He) dan diberi lambang  ⁴₂  α  atau  ⁴₂ He .

Sinar α memiliki sifat-sifat sebagai berikut:

a. bermuatan positif sehingga dalam medan listrik dibelokkan ke kutub

negatif;

b. daya tembusnya kecil (α < β < γ );

c. daya ionisasi besar (α > β > γ ).

2. Sinar Beta (β)

Sinar beta merupakan pancaran elektron dengan kecepatan tinggi dan

diberi lambang   ⁰₁β   atau   ⁰₁e.

Sinar beta memiliki sifat-sifat:

a. bermuatan negatif sehingga dalam medan listrik dibelokkan ke kutub positif;

b. daya tembusnya lebih besar dari α ;

c. daya ionisasinya lebih kecil dari α .

3. Sinar Gamma (γ)

Sinar gamma merupakan gelombang elektromagnetik dengan panjang gelombang yang pendek dan diberi lambang    ⁰₀γ  .

Sinar γ  memiliki sifat-sifat:

a. tidak bermuatan listrik, sehingga tidak dipengaruhi medan listrik;

b. daya tembusnya lebih besar dari α dan β;

c. daya ionisasi lebih kecil dari α dan β.

Selain sinar α , β dan γ unsur radioaktif juga memancarkan partikel yang lain, misalnya positron (elektron positif) ⁰₊₁e , neutron ¹₀n , proton ¹₁ p , detron ²₁D dan triton ³₁T .

Sinar α dan β dipengaruhi medanlistrik.

Daya tembus sinar α , β dan γ .

Bila unsur-unsur radioaktif memancarkan sinar α atau β maka akan berubah menjadi unsur lain.

• Bila unsur radioaktif memancarkan sinar α , akan menghasilkan unsur baru dengan nomor atom berkurang dua dan nomor massa berkurang empat.

Contoh:

²²⁶₈₈Ra  è  ²²²₈₆Rn  +  ⁴₂α

• Bila unsur radioaktif memancarkan sinar β , akan menghasilkan unsur baru dengan nomor atom bertambah satu dan nomor massa tetap.

Contoh:

²³⁴₉₀Th è  ²³⁴₉₁Pa   +  ⁰_-1β

Pemancaran sinar γ dari unsur radioaktif tidak menghasilkan unsur baru.

C. Stabilitas Inti

Dalam inti atom terdapat proton dan neutron yang disebut nukleon (partikel penyusun inti). Suatu inti atom (nuklida) ditandai jumlah proton dan jumlah neutron. Secara umum nuklida dilambangkan dengan:

^A X

^Z           

dimana è   A = nomor massa = jumlah proton + jumlah neutron

Z = nomor atom = jumlah proton

Kestabilan inti ditentukan oleh imbangan banyaknya proton dan neutron,

karena neutron dalam inti berfungsi menjaga tolak-menolak antar proton.

Untuk unsur yang kecil, jumlah neutron sama atau sedikit lebih banyak dari pada proton.

Untuk unsur yang berat jumlah neutron lebih banyak daripada  proton.

Contoh :

Nuklida yang stabil dengan nomor atom terbesar 83 yaitu ²⁰⁹₈₃ Bi, sedangkan nuklida dengan Z > 83 tidak stabil.

Sampai dengan nomor atom 80 inti-inti stabil semakin besar angka banding

neutron dengan proton.

 Inti ⁴⁰₂₀Ca adalah inti stabil terberat yang angka banding neutron-protonnya adalah 1.

Inti yang tidak stabil (bersifat radioaktif) memiliki perbandingan n/p di luar pita kestabilan, yaitu:

1. di atas pita kestabilan

2. di bawah pita kestabilan

3. di seberang pita kestabilan

D. Peluruhan

Inti yang tidak stabil akan mengalami peluruhan yaitu proses perubahan dari inti yang tidak stabil menjadi inti yang lebih stabil.

Inti yang terletak di atas pita kestabilan, memiliki harga n/p terlalu besar (kelebihan neutron), akan mencapai kestabilan dengan cara:

a. Memancarkan sinar (elektron)

Pada proses ini terjadi perubahan neutron menjadi proton.

¹₀n è   ¹₁ p +   ⁰_-1 e

Contoh:

¹⁴₆C è ¹⁴₇N + ⁰_-1 e

³⁵₁₆S è ³⁵₁₇ Cl + ⁰_-1 e

¹³⁷₅₅Cs è ¹³⁷₅₆Ba + ⁰_-1 e

b. Memancarkan neutron

Proses ini jarang terjadi di alam, hanya beberapa inti radioaktif yang mengalami proses ini.

Contoh:

⁵₂He è ⁴₂He + ¹₀ n

Inti yang terletak di bawah pita kestabilan memiliki harga n/p yang terlalu kecil (kelebihan proton), akan mencapai kestabilan dengan cara:

a. Memancarkan positron

Pada proses ini terjadi perubahan proton menjadi netron.

¹₁ p è ¹₀ n + ⁰₁e

Contoh:

¹¹₆C è¹¹₅B + ⁰₁e

b. Memancarkan proton (proses ini jarang terjadi)

Contoh:

³³₁₆S è ³²₁₅P + ¹₁p

c. Menangkap elektron

Elektron terdekat dengan inti (elektron di kulit K) ditangkap oleh inti atom sehingga terjadi perubahan

¹₁ p + ⁰_-1 e ==> ¹₀ n

Contoh:

⁴⁰₁₉K + ⁰₊₁e è ⁴⁰₁₈Ar

⁹⁰₄₂Mo + ⁰_-1e è ⁹⁰₄₁Nb

Inti yang terletak di seberang pita kestabilan (Z > 83) mencapai kestabilan dengan cara memancarkan alfa.

Contoh:

²¹⁶₈₄Po è ²¹²₈₂Pb  +  ⁴₂α

E. Kecepatan Peluruhan

Telah kita pelajari bersama bahwa nuklida yang tidak stabil akan mengalami peluruhan menjadi nuklida yang lebih stabil. Kecepatan  peluruhan tiap nuklida berbeda-beda tergantung jenis nuklidanya. Bila ditinjau dari segi orde reaksi, peluruhan nuklida radioaktif mengikuti reaksi

orde satu. Hal ini dapat kita gambarkan sebagai berikut:

Bila N adalah jumlah zat radioaktif pada waktu t, maka jumlah yang  terurai tiap satuan waktu dapat dinyatakan dengan persamaan diferensial, yaitu:

_ dN  = λ N

dt

, dimana λ = tetapan peluruhan, yang besarnya tergantung jenis zat radioaktif.

 Bila persamaan di atas diintegralkan akan menjadi:

N = N₀e^- λ t ,

 dengan N0 = jumlah zat radioaktif pada saat t = 0 (mula-mula).

Pada gambar di atas tampak bahwa setelah waktu t jumlah zat radioaktif menjadi ½ dari jumlah pemula. Dalam hal ini kita mengenal  waktu yang diperlukan oleh zat radioaktif untuk meluruh menjadi separuh  (setengah) dari jumlah semula, yang dikenal dengan waktu paruh (t ½ ).

Jadi, pada saat t = t ½  , maka N = ½ N0 ,

Sehingga :

1  =    0,693

   2           λ

Bila  :

jumlah zat radioaktif mulamula = N0 dan waktu paruh = t1/2,

maka setelah waktu paruh pertama  jumlah zat radioaktif tinggal  1/2N0

dan setelah waktu paruh kedua tinggal ¼ N0.

Setelah zat radioaktif meluruh selama waktu t, maka zat radioaktif yang tinggal (N), dapat dirumuskan dengan:

           

             t 

N  =  1  t^1/2    X  N₀

         2

Contoh Soal :

1. Suatu zat radioaktif x sebanyak 12,8 gram dan memiliki waktu paruh 2 tahun. Berapa gram zat radioaktif x yang tersisa setelah 6 tahun?

Jawab:

Diketahui: N0 = 12,8 gram, t ^1/2      = 2 tahun, t = 6 tahun

                 

Ditanyakan:  N = ...

             t 

N  =  1  t^1/2    X  N₀

         2

             6 

N  =  1   ²    X  12,8

         2

             

N  =  1  ³    X  12,8

         2

N  =  1     X  12,8  = 1,6 gram

         8

2. Suatu radioisotop memiliki massa 8 mg. Setelah beberapa hari, massanya berkurang menjadi 2 mg. Jika waktu paruh radioisotop tersebut 20 hari, telah berapa lamakah radioisotop tersebut meluruh?

Jawab

Diketahui

Nt = 2 mg

N0 = 8 mg

t 1/2 = 20 hari

Nt = ( 1/2 )ⁿ x N0

2 = ( 1/2 )ⁿ x 8

( 1/2 )ⁿ = 1/4

n = 2

n =   t

       t^1/2

t = n × t 1/2 = 2 x 20 = 40

Jadi, radioisotop tersebut telah meluruh selama 40 hari.

TRANSFORMASI GEOMETRI

Oleh : Risa Gestiana

Riie.com

بِسْــــــــــــــــــمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ

Transformasi geometri atau secara bahasa berarti perubahan. Pengertian panjangnya yaitu perubahan pada sebuah bidang geometri yang mencantum posisi, besar dan bentuknya sendiri.

Apabila hasil transformasi kongruen dengan bangunan yang ditranformasikan, maka hal itu disebut sebagai transformasi isometri.

Transformasi isometri sendiri mempunyai dua jenis yaitu transformasi isometri langsung serta transformasi isometri berhadapan.

Transformasi isometri langsung meliputi translasi dan rotasi, sementara untuk transformasi isometri berhadapan termasuk refleksi.

Transformasi Geometri

Transformasi geometri adalah suatu perubahan posisi (perpindahan) dari suatu posisi awal (x , y)menuju ke posisi lain (x’ , y’).

Transformasi geometri terbagi menjadi empat jenis, antara lain:

Jeni-jenis Transformasi Geometri:

1. Translasi (pergeseran)
   
2. Refleksi (pencerminan)
3. Rotasi (perputaran)
4. Dilatasi (perkalian)

Untuk lebih jelasnya mengenai jenis dari transformasi geometri di atas, yuk simak ulasannya berikut ini.

Jenis-jenis Transformasi Geometri

1. Translasi (Pergeseran)

Translasi adalah salah satu jenis transformasi yang berguna untuk memindahkan suatu titik sepanjang garis lurus dengan arah dan jarak.

Yang berarti, translasi tersebut hanya akan mengalami perpindahan titik ya guys.

Penentuan hasil objek lewat translasi cukup mudah. Caranya hanya dengan cara menambahkan absis serta ordinat dengan jarak tertentu sesuai dengan ketentuan tertentu.

Untuk lebih jelasnya tentang proses translasi bisa dilihat pada gambar di bawah.

Sebagai contoh:

Jika kalian perhatikan baik-baik, apabila kita sedang naik perosotan, perosotan itu hanya akan mengubah titik awal (puncak perosotan), menuju titik akhir (ujung perosotan).

Berikut adalah gambaran dari translasi:

Dari gambar di atas, dapat kita ketahui bahwa translasi hanya dapat berubah posisinya saja. Ukuran akan tetap sama.

Adapun rumus dari translasi, yaitu:

(x’ , y’) = (a , b) + (x , y)

Keterangan:

• (x’ , y’) = titik bayangan
• (a , b) = vektor translasi
• (x , y) = titik asal

2. Refleksi (Pencerminan)

Pembahasan selanjutnya yaitu pencerminan atau yang biasa kita kenal dengan sebutan refleksi.

Sama halnya dengan bayangan benda yang terbentuk pada sebuah cermin. Suatu objek yang mengalami refleksi akan mempunyai bayangan benda yang dihasilkan oleh suatu cermin.

Hasil dari refleksi pada bidang kartesius tergantung sumbu yang menjadi cerminnya.

Refleksi tersebut akan memindahkan seluruh titik dengan memakai sifat pencerminan pada cermin datar.

Coba lihatlah garis dan juga beberapa titik merah gambar di atas. Garis dan juga titik-titik merah tersebut berpindah hal itu sama seperti yang ada pada benda yang dihadapkan pada cermin datar.

Sama halnya dengan translasi, refleksi juga mempunyai rumus tersendiri lho. Berikut informasi selengkapnya.

Rumus Umum Refleksi

1. Pencerminan terhadap sumbu -x : (x,y) → (x, -y)
2. Pencerminan terhadap sumbu -y : (x,y) → (-x, y)
3. Pencerminan terhadap garis y = x : (x,y) → (y,x)
4. Pencerminan terhadap garis y = x : (x,y) → (-y, -x)
5. Pencerminan terhadap garis x = h : (x,y) → (2h -x,y)
6. Pencerminan terhadap garis y = k : (x,y) → (x, 2k – y)

Selain itu, pembahasan materi refleksi juga memuat tujuh jenis refleksi.

Jenis tersebut diantaranya yaitu: refleksi terhadap sumbu x, sumbu y, garis y = x, garis y = -x, titik O (0,0), garis x = h, dan garis y = k.

Berikut ini adalah ringkasan daftar matriks transformasi yang ada di refleksi atau pencerminan.

Kemudian, mari perhatikan uraian matriks transformasi untuk masing-masing jenisnya.

Pencerminan terhadap sumbu x

Pencerminan Terhadap Sumbu y

Pencerminan terhadap Garis y = x

Pencerminan terhadap Garis y = – x 

Pencerminan terhadap Titik Asal O(0,0)

Pencerminan terhadap Garis x = h

Pencerminan terhadap Garis y = k

3. Rotasi (Perputaran)

Rotasi atau perputaran adalah sautu perubahan kedudukan atau posisi objek dengan cara diputar lewat suatu pusat dan sudut tertentu.

Besarnya rotasi dalam transformasi geometri sebesar α yang telah disepakati untuk arah yang berlawanan dengan arah jalan jarum jam.

Apabila arah perputaran rotasi pada sebuah benda searah dengan jarum jam, maka sudut yang dibentuk yaitu -α.

Hasil dari rotasi sebuah objek tergantung dari pusat serta besar sudut rotasi. Perhatikan perubahan letak kedudukan segitiga yang diputar sebesar 135° dengan pusat o(0,0) pada gambar di bawah ini.

Di kehidupan nyata, bianglala yang sering kita lihat di tempat rekreasi merupakan salah satu contoh dari rotasi dalam transformasi geometri lho. 

Prinsip yang digunakan sama dengan rotasi dalam transformasi geometri, dimana memutar pada sudut serta titik pusat tertentu yang mempunyai jarak sama dengan setiap titik yang diputar.

Adapun rumus yang digunakan dalam rotasi transformasi geometri, antara lain:

• Rotasi sebesar 90° dengan pusat (a,b) : (x,y) → (-y + a+b, x -a + b)
• Rotasi sebesar 180° dengan pusat (a,b) : (x,y) → (-x + 2a+b, -y + 2b)
• Rotasi sebesar -90° dengan pusat (a,b) : (x,y) → (y – b + a, -x + a + b)
• Rotasi sebesar 90° dengan pusat (0,0) : (x,y) → (-y, x)
• Rotasi sebesar 180° dengan pusat (0,0) : (x,y) → (-x, -y)
• Rotasi sebesar -90° dengan pusat (0,0) : (x,y) → (y, -x)

Memperoleh hasil rotasi dengan cara menggambarnya terlebih dulu akan sangat tidak efektif.

Maka dari itu kita harus menggunakan metode lain yang bisa digunakan untuk menentukan hasil objek hasil rotasi. Solusinya adalah dengan cara memakai rumus transformasi geometri untuk rotasi.

Simak lebih lanjut rumusnya pada pembahasan di bawah ini.

Rotasi dengan Pusat o(0,0) sebesar α

Rotasi dengan Pusat (m,n) sebesar α

Rotasi dengan pusat (0,0) sebesar α kemudian sebesar β

Rotasi dengan pusat P(m,n) sebesar α kemudian sebesar β

4. Dilatasi (Perkalian)

Dilatasi juga dikenal dengan sebagai perbesaran atau pengecilan sebuah objek.

Apabila transformasi pada translasi, refleksi, serta rotasi hanya mengubah posisi benda, maka lain halnya dengan dilatasi yang melakukan transformasi geometri dengan cara merubah ukuran benda.

Ukuran benda bisa akan dibuah oleh dilatasi menjadi lebih besar atau lebih kecil. Perubahan ini bergantung pada skala yang menjadi faktor dari pengalinya.

Dilatasi bisa dipahami sebagai bentuk pembesaran atau pengecilan dari titik-titik yang membentuk sebuah bangun.

Berikut adalah ilustrasi dari dilatasi:

Rumus pada dilatasi ada dua yang dibedakan menurut pusatnya. Perhatikan uraian rumus untuk transformasi geometri pada dilatasi yang ada di bawah.

Dilatasi titik A(a, b) pada pusat O(0,0) dengan faktor skala m

Dilatasi titik A9(a,b) terhadap pusat P(k,l) dengan faktor skala m

Contoh Soal & Pembahasan

 

1. Bayangan garis y = 2x + 2 yang dicerminkan terhadap garis y= x adalah. . .

Jawaban : C

Pembahasan : 

2. Persamaan bayangan kurva y = x² – 2x – 3 oleh rotasi [0, 180°], kemudian dilanjutkan oleh pencerminan terhadap garis y = -x adalah …. 

A. y = x² – 2x – 3 

B. y = x² – 2x + 3

C. y = x² + 2x + 3

D. x = y² – 2y – 3

E. x = y² + 2y + 3

Jawaban : D

Pembahasan : 

Rotasi sudut-sudut yang lain dapat dihitung sendiri menggunakan kaidah trigonometri.

pencerminan terhadap garis y = -x

3. Persamaan bayangan dari lingkaran x² +y² +4x – 6y – 3 = 0 oleh transformasi yang berkaitan dengan matriks

adalah…. 

A. x² + y² – 6x – 4y- 3 = 0

B. x² + y² – 6x + 4y- 3 = 0

C. x² + y² + 6x – 4y- 3 = 0

D. x² + y² – 4x + 6y- 3 = 0

E. x² + y² + 4x – 6y+ 3 = 0

Jawaban : A

Pembahasan :

4. Bayangan titik A (4,1) oleh pencerminan terhadap garis x =2 dilanjutkan pencerminan terhadap garis x = 5 adalah titik…. 

A. A” (8,5) 

B. A” (10,1)

C. A” (8,1) 

D. A” (4,5)

E. A” (20,2)

Jawaban : B

Pembahasan :

5. Persamaan peta kurva y = x² – 3x + 2 karena pencerminan terhadap sumbu x dilanjutkan dilatasai dengan pusat O dan factor skala 3 adalah…

A. 3y + x² – 9x + 18 = 0

B. 3y – x² + 9x – 18 = 0

C. 3y – x² + 9x + 18 = 0

D. 3y + x² + 9x + 18 = 0

E. y + x² + 9x – 18 = 0 

Jawaban : A

Pembahasan :

pencerminan terhadap sumbu x:

P ( x , y ) → P ‘ ( x , – y )

Dilatasi terhadap titik pusat O(0,0) dengan factor skala 3 :

[O, k] : P(x,y) → P'(kx, ky)

[O,3k] : P(x,y) → P'(3x, 3y)

pencerminan terhadap sumbu x dilanjutkan dilatasi dengan pusat O dan factor skala 3 :

P(x,y) → P ‘(x, -y) → P ”(3x, -3y)

6. Tentukan bayangan lingkaran (x-3)² + (y+1)² = 4 jika ditranslasikan 

a. 5

b. 4

c. 3

d. 2

e. 1

Jawaban : B

Pembahasan : 

Ambil sembarang titik P(a,b) pada lingkaran (x-3)2 + (y+1)2 = 4 sehingga diperoleh (a-3)2 + (b+1)2 = 4

7. Titik A(a,b) dicerminkan terhadap garis x=2 menghasilkan bayangan titik A’(0,2), maka nilai (a,b) berturut-turut adalah….

a. 2 , 4

b. 4 , 2 

c. 2 , 2

d. 3 , 1

e. 1 , 3

Jawaban : B

Pembahasan :

8. Tentukan persamaan peta dari garis 3x – 5y + 15 = 0 oleh pencerminan terhadap sumbu x!

Pembahasan :

9. Tentukan persamaan peta dari garis 3x-5y+15=0 oleh dilatasi terhadap pusat O(0,0) dengan faktor skala 5!

Pembahasan :

10. Lingkaran x² + y² – 6x + 2y + 1 = 0. Jika ditransformasikan dengan dilatasi [O,4], persamaan bayangannya adalah….

Pembahasan :

Transformasi geometri atau sering disebut geometri adalah mengubah setiap koordinat titik (titik-titik dari suatu bangun) menjadi koordinat lainnya pada bidang dengan suatu aturan tertentu. Misalnya, transformasi T terhadap titik P (x,y) menghasilkan bayangan P’ (x’,y’)

BILANGAN

Oleh : Risa Gestiana

Riie.com

بِسْــــــــــــــــــمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ

MATEMATIKA KELAS VII SEMESTER 1 : BAB 1 Bilangan

1. Pengertian Bilangan Bulat

Bilangan bulat terdiri dari

- bilangan asli : 1, 2, 3, ...
- bilangan nol : 0
- bilangan negatif : ..., -3, -2, -1
Bilangan Bulat dinotasikan dengan : B = {..., -3, -2, -1, 0, 1, 2, 3, ...}
Bilangan lain yang berada dalam bilangan bulat, di antaranya adalah bilangan:
a. Cacah : C = {0, 1, 2, 3, 4, ...}
b. Ganjil : J = {1, 3, 5, 7, ...}
c. Genap : G = {2, 4, 6, 8, ...}
d. Cacah Kuadrat : K = {0, 1, 4, 9, ...}
e. Prima : {2, 3, 5, 7, 11, ...}


2. Membandingkan Bilangan Bulat

Dengan memperhatikan tempat pada garis bilangan, dapat kita nyatakan (dalam contoh) bahwa:
a. 7 > 4, karena 7 terletak di sebelah kanan 4,
b. (-5) < 2, karena (-5) terletak di sebelah kiri 2, dan lain sebagainya.


3. Penjumlahan dan Sifatnya
Salah satu Rumus penting :

Contoh : 7 + (-10) = 7 - 10 = -3
Sifat-sifatnya :
a. Komutatif :

b. Asosiatif :

c. Tertutup :

d. Memiliki identitas :

e. Invers penjumlahan :

4. Pengurangan
Pengurangan merupakan lawan (invers) dari penjumlahan.
Rumus :

Contoh : 8 - (-2) = 8 + 2 = 10


5. Perkalian dan Sifatnya
contoh :
3 x (-2) = (-2) + (-2) + (-2)

Sifat-sifat :

6. Pembagian
Pembagian adalah kebalikan (invers) dari perkalian.
Rumus :

7. Perpangkatan dan Sifat

8. Akar Pangkat Dua dan Akar Pangkat Tiga

9. Bentuk Pecahan

Contoh Soal & Pembahasan

Latihan Soal